NAND as Universal Gate

NAND Gate 又叫与非门，可以理解为与门和非门的组合，用逻辑表达式为： $Y=\overline{a\cdot b}$

NAND as NOT

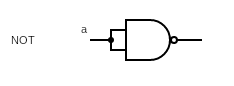
NOT 是一个单输入的逻辑门，用逻辑表达式为： $Y=\overline{a}$ 。

因为 $a\cdot a = a$ 所以 $Y = \overline{a\cdot a} = \overline{a}$

/**
 * Not gate:
 * out = not in
 */

CHIP Not {
    IN in;
    OUT out;

    PARTS:
    // Put your code here:
    Nand(a = in, b = in, out = out);
}

NAND as AND

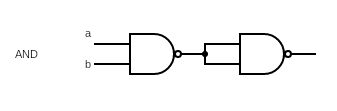
AND Gate 是一个两输入的逻辑门，用逻辑表达式为： $Y=a\cdot b$ , 其中 $a$ 和 $b$ 分别是输入的两个端口。

NAND Gate 逻辑表达式为： $Y=\overline{a\cdot b}$ ，我们想要得到 $a\cdot b$ ，只需要对 $Y$ 做一个取反操作即可，即： $Y' =\overline{\overline{a\cdot b}} = a\cdot b$

/**
 * And gate:
 * out = a and b
 */

CHIP And {
    IN a, b;
    OUT out;

    PARTS:
    // Put your code here:
    Nand(a = a, b = b, out = nandOut);
    Nand(a = nandOut, b = nandOut, out = out); // Not(in = nandOut, out = out);

NAND as OR

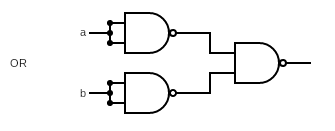
OR Gate 是一个两输入的逻辑门，用逻辑表达式为： $Y=a+b$ , 其中 $a$ 和 $b$ 分别是输入的两个端口。

NAND Gate 逻辑表达式为： $Y=\overline{a\cdot b}$ ，根据 DeMorgan's law，我们可以得到 $Y = \overline{a\cdot b} = \overline{a}+\overline{b}$ ，那如果我们在输入 $a$ 和 $b$ 的时候，分别对他们进行取反操作让输入变成 $\overline{a}$ 和 $\overline{b}$ , 则可得到：

Y=\overline{\overline{a}\cdot \overline{b}} = \overline{\overline{a}}+\overline{\overline{b}}=a+b

/**
 * Or gate:
 * out = a or b
 */

CHIP Or {
    IN a, b;
    OUT out;

    PARTS:
    // Put your code here:
    Nand(a = a, b = a, out = nota);
    Nand(a = b, b = b, out = notb);
    Nand(a = nota, b = notb, out = out);
}

NAND as NOR

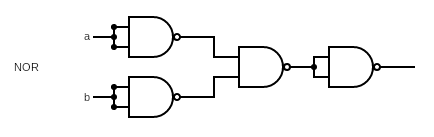
NOR Gate 是一个两输入的逻辑门，用逻辑表达式为： $Y=\overline{a+b}$ , 其中 $a$ 和 $b$ 分别是输入的两个端口。

上面已经有了 OR 的实现和 NOT 的实现，直接用 OR 和 NOT 就可以得到 NOR 的实现，即：

/**
 * Nor gate:
 * out = a nor b
 */

CHIP Nor {
  IN a, b;
  OUT out;

  PARTS:
  // Put your code here:
  //Or(a = a, b = b, out = out);
  Nand(a = a, b = a, out = nota);
  Nand(a = b, b = b, out = notb);
  Nand(a = nota, b = notb, out = orOut);
  Nand(a = orOut, b = orOut, out = out);

NAND as XOR

XOR Gate 是一个两输入的逻辑门，用逻辑表达式为： $Y=a\oplus b=a\cdot \overline{b}+\overline{a}\cdot b$ , 其中 $a$ 和 $b$ 分别是输入的两个端口。

这里我们需要用到两个 AND，两个 NOT，一个 OR，所以一共需要九个Nand，即：

/**
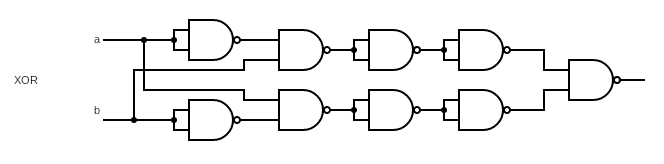
 * Xor gate:
 * out = a xor b
 */

CHIP Xor {
  IN a, b;
  OUT out;

  PARTS:
  // Put your code here:
  Nand(a = b, b = b, out = notb);
  Nand(a = a, b = notb, out = nandanotb);
  Nand(a = nandab, b = nandab, out = aandnotb);
  Nand(a = a, b = a, out = nota);
  Nand(a = nota, b = b, out = nandnotab);
  Nand(a = nandnotab, b = nandnotab, out = notaandb);
  Nand(a = aandnotb, b = aandnotb, out = NOTaandnotb);
  Nand(a = notaandb, b = notaandb, out = NOTnotaandb);
  Nand(a = NOTaandnotb, b = NOTnotaandb, out = out);
}

这个实现用到了过多的 NAND，我们想办法优化一下，注意观察图中红框里的部分，这部分是明显就是两次 NOT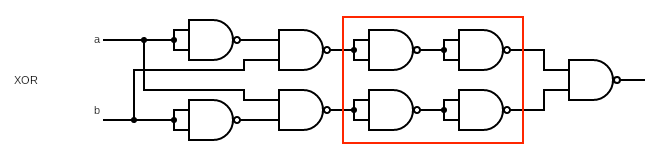：这两次 NOT 叠加之后就相当于什么事情都没干，所以我们可以把这部分干掉，就剩下五个 Nand，即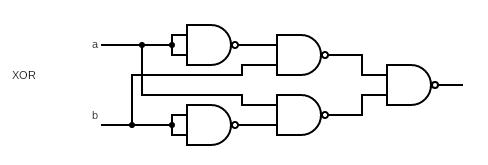：其实我们还可以对这个门进行一次简化，用四个 NAND 来实现 XOR（这里如果全部用逻辑运算写的话太复杂，我直接在公式里使用 NAND 了）:

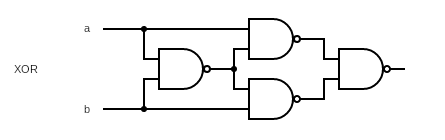
\begin{aligned} Y &=a\oplus b\\ & =a\cdot \overline{b}+\overline{a}\cdot b\\ & =NAND\big(\overline{(a\cdot \overline{b})}, \overline{(\overline{a}\cdot b)}\big)\\ & =NAND(\overline{a}+b, \overline{b}+a)\\ & =NAND\big(\overline{a}+(a\cdot b), \overline{b}+(a\cdot b)\big)\\ & =NAND\Big(NAND\big(a\cdot (\overline{a\cdot b})\big), NAND\big(b\cdot (\overline{a\cdot b})\big)\Big)\\ & =NAND\Bigg(NAND\Big(a\cdot\big(NAND(a,b)\big)\Big), NAND\Big(b\cdot\big(NAND(a,b)\big)\Big)\Bigg)\\ \end{aligned}

/**
 * Xor gate:
 * out = a xor b
 */
CHIP Xor {
  IN a, b;
  OUT out;
  PARTS:
  // Put your code here:  Nand(a = a, b = b, out = nandAB);
  Nand(a = a, b = nandAB, out = nandABA);
  Nand(a = b, b = nandAB, out = nandABB);
  Nand(a = nandABA, b = nandABB, out = out);